TL;DR, Bitcoin has never been anonymous since its inception. Making it more private becomes one of the most vibrant research areas in the space. While some proposals have made (or are making) their way into the Bitcoin’s reference implementation, others were either implemented in altcoins or get abandoned altogether. In this post, the following privacy enhancing technologies are categorized and surveyed based on the information they are trying to hide.

• Reciever: HD Wallet, Stealth Address, Resusable Payment Code, Coin Control, etc
• Sender: Centralized Mixer, CoinJoin and its variants, CoinShuffle, TumbleBit, Ring Signatures, etc
• Amount: Rounds Based Fixed Demonimation Mixing, Unequal Input Mixing, Confidential Transactions, Mimblewimble, etc
• Transasction Logic: P2SH, Merkle Branches (MAST), Schnorr Signatures, Taproot, Graftroot, etc

Network layer privacy technologies such as Dandelion or Peer to Peer Encryption are not discussed. Neither is the privacy benefits of the Layer 2 systems to the base layer. Technologies related to ZCash are also intentionally left out.

Bitcoin whitepaper has a section dedicated to privacy, in which it states:

The traditional banking model achieves a level of privacy by limiting access to information to the parties involved and the trusted third party. The necessity to announce all transactions publicly precludes this method, but privacy can still be maintained by breaking the flow of information in another place: by keeping public keys anonymous.

It becomes clear over the years that Bitcoin has never achieved the level of privacy that people had hoped for. A Bitcoin transaction consists of 4 pieces of sensitive information: sender, reciever, amount and transaction logic (written in Bitcoin Script), all of which are broadcasted to the Bitcoin network and stored in the blockchain forever because the only way to confirm the absence of a transaction is to be aware of all transactions. It is debatable if recording all aspects of a transaction without much protection is the only way (or even the best way) to “be aware” of it, but the fact that all transactions are transparent in the Bitcoin blockchain means that if Alice’s real life identity is somehow tied a Bitcoin address, she will lose the privacy of all her past and future transactions associated with that address.

Most of the privacy technologies in Bitcoin are designed to obfuscate one or more of the sensitive transaction information from the blockchain, each making different set of tradeoffs. A few things should perhaps be taken into account when evaluating them.

• Decentralization means security is the result of public verification, which is often at odds with privacy. Fortunately, this apparent conflict is not always true, but it is still important to evaluate if a privacy enhancing technology comes at the cost of centralization.
• Privacy and scalability don’t always play well together. Many privacy technologies require much more computational resources which gets dramatically magnified in the context of blockchain, affecting it’s ability to scale. Others break pruning, resulting in ever growing database to verify new transactions. Luckily, this is not always true either.
• Privacy technologies could damage user experience due to heavier computation and longer verification time or complex interaction with other users. No matter how perfect a privacy technology is in theory, it doesn’t generate any real world value if nobody uses it due to bad UX.

The rest of the post is divided up into 4 sections: Receiver, Sender, Amount and Transaction Logic, in which the relevant privacy technolgies are discussed.

Receiver

Hierarchical Deterministic Wallets

Assuming Alice uses an unique Bitcoin address all the time and this address somehow gets tied back to her real world identity, Alice’s entire transaction history on Bitcoin network will become public. One way to mitigate this problem is to generate a fresh receiving address for each incoming transactions, which is a pretty safe and easy operation if Alice uses one of those HD Wallets. This way, to piece together Alice’s transaction history, attackers need to tie all of those addresses together to Alice’s identity, which is not impossible but significantly harder. In fact, use new address to receive this payment is a best practice when using bitcoin, including change addresses.

Stealth Address

In scenarios such as TV or billboard ads, where generating a fresh receiving address is not an option, stealth address might offer a solution. The idea is that after Alice publishes her public key, whoever wants to pay her needs to take that information, generate and “pay” to a new public key whose corresponding private key can only be derived by Alice. One way to achieve this is by leveraging the ECDH protocol.

Assuming that Alice’s keypair is A=aG where G is the base point of an Eliptic Curve, Bob first needs to generate a ephemeral keypair B=bG. With ECDH protocol, the shared secrets between Alice and Bob is secret=bA=aB=abG. Bob then pays to the new address derived from A+H(secret)G where H is a cryptographic hash function. Since only Alice knows a+H(secret), she is the only one who can spend the fund in this new address.

In reality, as described by Bitcoin developer Peter Todd, it requires Bob to make an extra transaction with OP_RETURN to essentially communicate the ephemeral public key B to Alice so that she can derive the shared secret. But according to him later on, OP_RETURN was changed at last minute to only include 40 bytes of data, so the stealth address BIP (BIP 63) was never published. Overall, stealth address is not well adopted in the Bitcoin ecosystem, DarkWallet seems to support it but the project is not actively maintained any more. Monero and TokenPay on the other hand introduced a more interesting version of stealth address which enables the seperation of view key and spend key by utilizing the Dual-Key Stealth Address Protocol. This is very useful when transaction history need to be inspected by third parties without giving them the ability to spend the fund.

Resusable Payment Code

Resumable Payment Code protocol tries to achieve the same result as Stealth Address using the combination of ECDH protocol and HD Wallets.

Assuming that Alice and Bob want to transact in a private manner without sending each other new addresses all the time, both of them can generate a resuable payment code which is essentially extended public key in the context of HD Wallets. Alice communicates her payment code through a notification transaction to Bob first, and from that point on Alice and Bob shares a secret based on the same ECDH protocol used in Stealth Address.

With this shared secret and the resuable payment codes from each other, Alice and Bob could generate a new HD wallet respectively where they can only spend their own fund but both of them know how to derive new addresses for each other. This essentially builds up a secret payment tunnel between themselves.

Samourai is one of the wallets that support Reusable Payment Code.

Coin Control

If two outputs are spent by the same transaction, they usually belong to the same owner (except for e.g. CoinJoin transactions). If one of them happens to be tainted, the other one will be considered tainted as well. Coin Control gives users the option to pick which combinations of outputs to use when constructing a transaction, which could reduce the chance of accidentally tainting outputs.

Many wallets supports the coin control feature, including the Bitcoin Core wallet.

Sender

To obfuscate the sender of a transaction, the general idea is to hide it among other senders or decoys and make it hard for the attacker to figure out which one actually sends the fund to your receiver.

The key observation in Bitcoin is that inputs and outputs in a transaction are independent of each other and there is no indication as to the linkage between inputs and outputs. Therefore if mutiple users construct one single transaction with their respective inputs and outputs, their funds are effectively mixed.

Image from https://bitcointalk.org/index.php?topic=279249.0

As illustrated above, it is hard to know whether the first output of transaction 2 is paid by its second input or the combination of its first and third inputs.

Centralized Mixer (aka Tumbler)

One approach is to have centralized mixing services taking funds from users and then mix them with other users’ funds and/or mixer’s own funds. If the mixer is well-intentioned, hopefully equal amount of funds (minus service fee) will be sent back to the users at new addresses. This idea is pretty straight forward, but its centralized nature means that it suffers the same set of problems as banks or centralized exchanges. Mixers could potentially steal users’ funds. It might also retain the ability to trace back where certain fund is originated. Mixing large amount of funds may be illegal in some jurisdictions, having a liable central entity might pose a larger regulatory risk.

There are also a lot of pitfalls even if the mixers are assumably trustworthy. One example is that if the amount of all the TXOs to be mixed are not the same, it becomes an extra piece of information to reveal who the sender is. Therefore it is advised to mix transactions with standard chunk sizes, which means that large amount of funds might require many rounds of mixing, creating bad user experience (to be fair, this is not unique to centralized mixers, without something like Confidential Transactions which hides the transaction amount, decentralized mixers suffer the same problem). Section 6.3 Mixing of the execellent book Bitcoin and Blockchain Technologies discussed some other potential implementation issues with centralized mixers at length, including a set of guidelines for them to provider better quality services for their users, such as multiple rounds of mixing.

Nonetheless, centralized mixers such as bestmixer.io might still be useful for people with certain threat models and risk profiles. Most users who decide to mix their coins still choose centralized mixing services.

CoinJoin

CoinJoin was proposed by Bitcoin developer Greg Maxwell in 2013, which removes the risk of theft by a third party.

To construct a CoinJoin transaction, a group of users need to somehow find each other, perhap through a centralized discovery service. Users then start to exchange their inputs and outputs to each other. Once all the inputs and outputs are collected, any user could use them to construct an unsigned version of a transaction and pass them around for everyone to sign. After everyone verified the correctness of the transaction and signed it off, the transaction could be broadcasted to the network.

Like centralized mixing, it is still important to make sure that all outputs has the same denomination. One of CoinJoin’s downsides is that it requires fair amount of user interactions, which not only hurts usability but also make it susceptible for sybil attacks. For example, attackers can join the group and try to learn the linkage between inputs and outputs. Even if inputs and outputs are exchanged on top of the anonymous communication protocols such as Tor, attackers can still reduce the size of the anonymity set if there are “users” controlled by them inside the group. DOS attack is also possible if attacker double spends any inputs in the CoinJoin transaction (which requires retry after removing the bad parties) or refuse to sign at the last stage (which could perhaps be addressed by a PoW like solution).

A variation of CoinJoin called Chaumian CoinJoin improves upon the original CoinJoin by leveraging blind signatures to ensure that even if there is a centralized service (like the coordinator in Wasabi Wallet), it is still not in a position to learn the linkage between inputs and outputs.

CoinShuffle attempts to address CoinJoin’s anomymity issue by running a clever decentralized protocols among participants. Assuming that Alice, Bob and Charlie are going to perform a CoinJoin and their freshly generated keys pairs are PubA/PrivA, PubB/PrivB and PubC/PrivC respectively. Following is how the CoinShuffle could be carried out.

• Alice is randomly selected to know PubA, PubB and PubC. Bob is randomly selected to know PubB and PubC. Charlie is randomly only knows PubB.
• Alice uses PubC to encrypt her output address and PubB to encrypt the encrypted message again. Alice sends the double encryted message to Bob.
• Bob recieves the double encrypted message from Alice, decrypt it using PrivB. Encrypt his own output address using PubC. Send both encrypted messages to Charlie.
• Charlie receives both encrypted messages, decrypts them using PrivC, revealing both Alice and Bob’s output addresses. He then uses them to construct the CoinJoin transaction together with his own output address

This onion structure similiar to Tor ensures that no parties involved knows the ownship of the outputs. Shufflepuff is an attempt to implement CoinShuffle in the Mycelium wallet, but the project doesn’t seem to be actively maintained any more.

In general, CoinJoin isn’t wildly used in the Bitcoin ecosystem yet. JoinMarket tries to tackle that problem by bringing economical incentives into the equation, but it hasn’t seen much adoption either. Bitcoin developer Jimmy Song recently recorded a video calling for easy to use CoinJoin, perhaps a breakthrough on the usability side is the key.

TumbleBit

Compared to CoinJoin, where funds are mixed in a single transaction. TumbleBit creates a linked payment channels between payer and payee through a centralized payment hub. The payment channels can be linked by leveraging Hashed Timelock Contract, which guarantees that the payment hub is unable to steal funds.

A blinded puzzle technique inspired by blind signatures is used to ensure that the payment hub can not establish the connection between payer and payee.

TumbleBit is currently integrated into the Breeze wallet from Stratis.

Ring signatures

Ring signature is worth mentioning here even though it would never be adopted by something like Bitcoin. It is an interesting digital signature scheme that can be used to implement a decentralized mixing service that requires no user interactions.

It is easy to verify that a ring signature is created by one of the members in a group but computationally infeasible to determine which one exactly. CryptoNotes based cryptocurrencies such as Monero takes advantage of this property to hide the senders of transactions. When constructing a transaction, currently 10 spent outputs are “randomly selected” by Monero from the blockchain as decoys along side with the real output. It will then:

• Derive a key image from the real output
• Generate a ring signature from this group of outputs.

Key image is unique for the same output even if it is mixed with different set of decoys. Monero blockchain keeps track of all the key images of the spent outputs to avoid double spends, thus breaking pruning. A valid ring signature means that one of the outputs in the group is authorized to be spent without revealing which one exactly.

Sender protection is considered to be the weakest part of Monero’s privacy scheme since there are a few known issues with ring signature such as 0 decoy and chain reaction, potential privacy breach during hard fork, etc. When it comes to decoys selection it is usually a cats and mouse game because it is very hard to predict all the heuristics. Nonetheless, it is still considered to be a technology that offers one of the strongest sender protection.

Amount

Transaction amount is not only by itself a very sensitive piece of information, it can also affect the effectiveness of other transaction graph obfuscation mechanisms such as CoinJoin or centralized mixers, etc. In general, to hide the amount, either transaction has to be split up into several smaller ones with uniform denomination, or else the amount needs to be hidden cryptographically in such a way that it is only known to the participants but everybody else can verify that no inflation is created during the transaction.

Rounds Based Fixed Demonimation Mixing

By agreeing on a set of standardized chunk sizes, mixers would increase the size of anonymity set for incoming transactions. It is also easier to apply a series of mixers as long as they agree on the same chunk sizes. The downside of this approach is that mixing a large amount of bitcoin might take a long time. For example, assuming the chunk sizes of a mixer is 0.1, 0.5 and 1 BTC, mixing 8.6 BTC requires a minimum of 10 rounds. Also, it might be impossible to mix a coin that is too smaller without merging it with others coins first.

Unequal Input Mixing

What if input amounts are allowed to be unequal, can outputs be split in such a way that the most optimal level of anonymity is preserved? If such algorithm exists, coins with smaller amounts no longer need to be merged before meeting mixers’s minimal chunk size. Coins with bigger amounts can also get matched together and enjoy much quicker mixing. Unequal input mixing attempts to address this issue but it is requires more research, though a basic form of it might be making its way into Wasabi Wallet in the near future.

Confidential transactions

Conceived by Adam Back and improved by Gregory Maxwell, Confidential Transactions offers a solution to hide transaction amount from the blockchain while keeping it verifiable that all transactions are balanced and no deliberate inflation was created.

To achieve this in a system like Bitcoin, it relies on a number of cryptographic constructs.

First off, confidential transaction hides amount using a commitment scheme called pederson commitment, which is a cryptographic primitive that not only allows one to “commit to a chosen value while keeping it hidden to others, with the ability to reveal the committed value later”, but also preserves the addition and commutative properties which is crucial for its application to ledger like systems:

Assuming that G and H are generator points of two elliptic curves, v is the transaction amount and r is a random number. Then

r*G + v*H

is a pederson commitment of the amount v. r is called a binding factor, which is essentially a big random number. if v == v1 + v2 and the corresponding pederson commitment for v1 and v2 are

r1*G + v1*H
r2*G + v2*H

respectively, then as long as r == r1 + r2, the entire pederson commit can be substracted to 0.

(r*G + v*H) - (r1*G + v1*H + r2*G + v2*H) == 0

This means that from the arithmetic point of view, the pederson commitment of an amount could be used as a replacement for amount in Bitcoin like systems. In fact, this is exactly what Element project has done.

This works except that if v1 is a negative number, v2 will be bigger than v, which means that coins are created out of thin air. Range proof solves this issue by proving that an amount is within a certain range, in the original confidential transaction post, range proof was designed to leverage Borromean ring signature. Later Bulletproofs was proposed to perform range proof in a much more efficent way.

One last piece of the puzzle is that if

r1*G + v1*H

is the amount of a transaction output, how would the recipient know the amount v1 and the binding factor r1? In Element, this is done through the classic ECDH key exchange. The output amount of a transction in Element actually contains not only the pederson commitment, but also a range proof and an ECDH ephemeral public key from the sender. With that, the receiver can derive the shared secret key with the sender, which can be used to unwind v1 and r1. A more detailed explanation from Pieter Wuille can be found here.

Since January 2017, Ring Confidential Transaction (RingCT) was implemented in Monero. Prio to that only outputs with the same denomination are allowed to be members of the same ring. With confidential transaction, not only the amount is hidden, the number of potential outputs that could be used as decoys becomes much larger as well.

Mimblewimble

Mimblewimble also uses confidential transaction to prove that transations are balanced without revealing the actual amounts. However, compared to Bitcoin like systems where a signature signed directly by a seperate private key is needed to prove the ownership of the output, it goes a bit further by leveraging the blinding factor instead.

Assuming that

ri*G + vi*H
ro*G + vo*H

are the pederson commitment of the input amount v1 and output amount v2. If v1 == v2, the substraction of the two commitment becomes (ro-ri)*G, which should be a valid public key. As long as the sender and receiver joinly produce a signature to prove that they know (ro-ri), the transaction is considered to be valid and the ownership of the coin is transfered. The ability to prove ownership like this enables cut-through, which turns out to be a further boost to MimbleWimble’s privacy and scalability.

Transaction Logic

Each output in a Bitcoin transaction has a condition that needs to be satisfied when an input attempts to spend it. When verifying a transaction, the concatenation of the input script and output script has to be evaluated to true. The most common spending condition is P2PKH, which can be resolved by providing a public key and a digital signature created by its corresponding private key.

Bitcoin Script can also be used to express more complex transaction logic, or smart contracts. One example is MultiSig in which an output requires more than one signature to get unlocked, often used as way to divide up the ownership of a coin. A 2-of-2 MultiSig example be found here.

From the perspective of privacy, having transaction logic transparently recorded on a public ledger is often times undesirable since it unnecessarily reveals the entire structure of the ownership.

P2SH

With P2SH an output can be sent to a script hash, which essentially shifts the burden of providing the complex transaction logic from the senders to the recipients. P2SH in itself is not a privacy enhancing technology since the same logic still needs to be provided by the recipient. But since usually a branch of logic is already decided at spending time, there is more room to maneuver when it comes to hiding information.

Merkle Branches (MAST)

One observation is that most of the transaction logic is just some disjunction of possibilities. Even though a coin can only be spent with one of the possible paths, the entire script with all possibilities needs to be revealed in the spending transaction input.

Merkle Branches (MAST) structures those possibilities as Merkle Tree. Assuming that Alice has a coin which she is allowed to spend at any time, but if the coin is not spent by her for 3 months, Bob and Charlie will be able to spend it together if they both agree. This could be expressed as following in Bitcoin Script:

OP_If
   <alice's pubkey> OP_CheckSig
OP_Else
   "3 months" OP_CSV OP_Drop
   2 <bob's pubkey> <charlie's pubkey> 2 OP_CheckMultiSig
OP_EndIf

(Credit: script and related images are from David A Harding’s execellent post about MAST)

With MAST, the above script could be structured as the following tree, with every square node containing a hash of the labels of its child nodes.

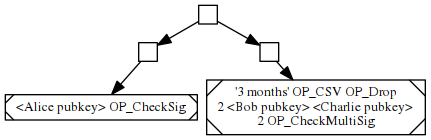
When Alice tries to spend the coin, only the left branch and the hash of the right branch need to be revealed. After three months, if Bob and Charlie decide to jointly spend the coin, they only need to reveal the right branch and the hash of the left branch.

From this example, the benefit of MAST when it comes to privacy and reducing transaction size is pretty obvious. David Harding’s post offers more in depth discussion.

Schnorr Signatures

Schnorr Signatures relies on the same security assumptions as ECDSA that it is hard to solve discret log problem. Compared to ECDSA which Bitcoin currently relies upon, the biggest advantage is that multiple schnorr signatures signed by different private keys for the same message can be verified by the sum of all the corresponding public keys. This is a significant property that could be leveraged to implement many interesting features, for example:

• Protocols can be devised to require only one aggregated signature to verify N-of-M MultiSig smart contract, which is a great win for privacy and scalability
• It offers better privacy for CoinJoin transaction since now all the participants only need to provide one joint signature. The resulting much smaller transaction could also serve as an extra economic incentives to perform CoinJoin.

Other features that could be implemented include batch verification, block level signature aggregation, etc. More information can be found here.

Taproot

Even though transaction logic might be composed of disjunction of posibilities, a key observation is that there usually can be a “unanimity branch” where the coin can be spent if every participant agrees. This is analogous to the court model in real life where even though it could enforce complex contract between different parties, in most of the scenarios it is just served as a deterrent. Normally transactions are resolved by mutual consensus off court.

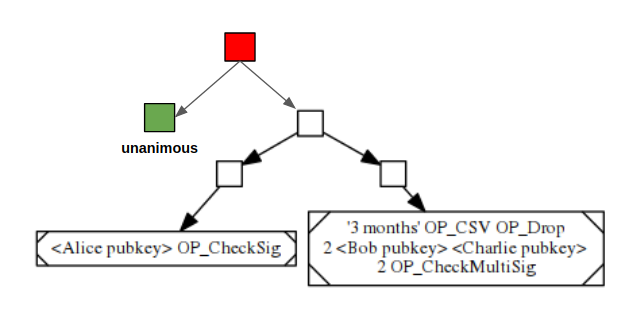
One approach to implement “unanimity branch” on top of MAST is to represent it as an extra branch alongside the original MAST tree, as shown in the green node above, and the red node would become the new merkle root. With schnorr signature, the red node could be reduced to just one signature. This could work, but every time when a transaction is settled with unanimity branch (which should be the most common scenario), the value of it still needs to be revealed, taking up the precious blockchain space.

Taproot is designed to represent the unanimity branch in a more efficient way. It is inspired by the idea of Pay-to-Contract by Timo Hanke. Assuming that the merkle root of a MAST script is C, and the aggregated public key of the unanimity branch is K, then the Taproot version of the script above would look like the following:

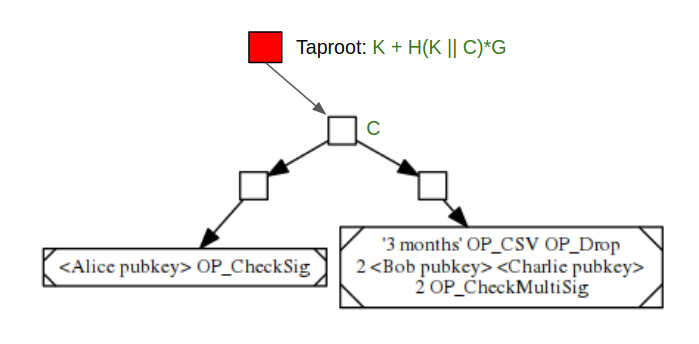
The Taproot node contains the value of K + H(K||C)*G, which can be spent in two ways:

• If unanimity branch is chosen, a signature signed by k + H(K||C) would be enough where k is the private key of K
• If no consensus is reached, C needs to be revealed and executed.

Since most transactions resolve with the unanimity branch, most Taproot transactions look just like a normal P2PKH transactions, with complex part of the transaction logic rarely revealed.

Graftroot

One of the limitations that Taproot suffers is that it only natively provides for one alternative. Graftroot was invented by Greg Maxwell to fix this limitation by using the delegation model.

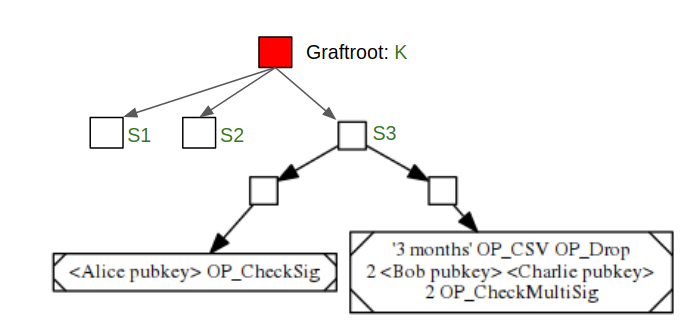
In the above example, K is the aggregated public key of the unanimity branch. S1, S2 and S3 are three alternative execution paths. There are two ways the transaction can be resolved:

• A signature signed by K’s corresponding private key k on the transaction.
• A signature signed by K’s corresponding private key k on either S1, S2 or S3, and the signed script needs to be successfully executed.

The second approach can be thought of as everybody involved decides to delegate the ownership to a script. In this way, any number of alternatives can be supported.

Many facinating privacy enhancing technologies for Bitcoin are being proposed and implemented. Hope this post helps you to understand this area a little bit better. Personally, I am looking forward to seeing Schnorr signatures and Taproot get implemented in Bitcoin soon. Perhaps confidential transaction too, but maybe that is too much of a wish :)